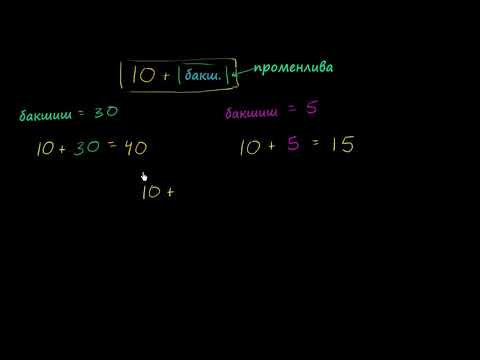
Съдържание
Когато писмо като а, б, х или ш изскача с математически израз, наречен променлива, но всъщност неговият заместител, който представлява редица неизвестна стойност. Можете да извършвате всички същите математически операции върху променлива, която изпълнявате на известен номер. Този факт е полезен, ако променливата изскочи във фракция, където ще ви трябват инструменти като умножение, деление и анулиране на общи фактори, за да опростите дроба.
Комбинирайте подобни термини както в числителя, така и в знаменателя на дроби. Когато за първи път започнете да боравите с дроби с променлива, това може да се направи за вас. Но по-късно може да срещнете „месие“ фракции като следното:
(а + а) / (2_a_ - а)
Когато комбинирате като термини, в крайна сметка получавате много по-цивилизована фракция:
2_a_ /а
Факторирайте променливата както от числителя, така и от знаменателя на дроби, ако можете. Ако променливата е фактор и на двете места, можете да я отмените. Помислете просто дадената опростена фракция:
2_a_ /а
Като бърз настрана, всеки път, когато видите променлива сама по себе си, се разбира, че има коефициент 1. Така че това може да се запише и като:
2_a_ / 1_a_
Което прави по-очевидно, че когато отмените общия фактор а както от числителя, така и от знаменателя на дроби, останахте със следното:
2/1
Което от своя страна опростява цялото число 2.
Ами ако имате дроб като 3_a_ / 2? Не можеш фактор а както от числителя, така и от знаменателя на дроби, но тъй като него е в числителя, можете да го третирате като цяло число. За да имате смисъл от това, първо изпишете фракцията по този начин:
3_a_ / 2 (1)
Можете да поставите 1 в знаменателя благодарение на свойството за мултипликативна идентичност, което заявява, че когато умножите всяко число по 1, резултатът ще бъде оригиналното число, с което сте започнали. Така че изобщо не сте променили стойността на фракцията; просто сте го написали малко по-различно.
След това разделете факторите по този начин:
а/1 × 3/2
И опростете а/ 1 до а, Това ви дава:
а × 3/2
Което може да бъде просто написано като смесено число:
а (3/2)
Какво ще стане, ако се окажете с разхвърлян фракция като следния?
(б2 - 9) / (б + 3)
На пръв поглед няма лесен начин за фактор б извън числителя и знаменателя. Да, б присъства и на двете места, но трябва да го извадите от фактор целия срок и на двете места, което би ви осигурило още по-меко б(б - 9/б) в числителя и б(1 + 3/б) в знаменателя. Това е задънена улица.
Но ако сте обърнали внимание на другите си уроци, може да забележите, че числителят всъщност може да бъде преписан като (б2 - 32), известен също като "разликата на квадратите", защото изваждате едно квадратно число от друго квадратно число. И има специална формула, която можете да запомните, за да разчетете разликата на квадратите. Използвайки тази формула, можете да пренапишете числителя, както следва:
(б - 3)(б + 3)
Сега, вижте това в кон на цялата фракция:
(б - 3)(б + 3) / (б + 3)
Благодарение на тази стандартна формула, която сте запомнили или потърсили, сега имате идентичния фактор (б + 3) както в числителя, така и в знаменателя на вашата дроб. След като отмените този фактор, вие оставате със следната част:
(б - 3) / 1
Което опростява само:
(б - 3)