
Съдържание
В геометрията осмоъгълник е многоъгълник с осем страни. Редовният осмоъгълник има осем равни страни и равни ъгли. Обикновеният осмоъгълник обикновено се разпознава по знаците за спиране. Октаедър е осемстранен многогранник. Обикновен октаедър има осем триъгълника с ръбове с еднаква дължина. Това е ефективно две квадратни пирамиди, които се срещат в техните бази.
Формула за зона на Октагон
Формулата за площта на обикновен осмоъгълник със страни с дължина "a" е 2 (1 + sqrt (2)) a ^ 2, където "sqrt" указва квадратния корен.
деривация
Един осмоъгълник може да се разглежда като 4 правоъгълника, един квадрат в центъра и четири равнобедрени триъгълника в ъглите.
Квадратът е с площ a ^ 2.
Триъгълниците имат страни a, a / sqrt (2) и a / sqrt (2), по теорията на Питагор. Следователно, всеки има площ от ^ 2/4.
Правоъгълниците са с площ a * a / sqrt (2).
Сумата от тези 9 области е 2a ^ 2 (1 + sqrt (2)).
Формула за обем на октаедър
Формулата за обема на обикновен октаедър от страни "а" е ^ 3 * sqrt (2) / 3.
деривация
Площта на четиристранна пирамида е площ на база * височина / 3. Следователно площта на правилен осмоъгълник е 2 * основа * височина / 3.
Основа = a ^ 2 тривиално.
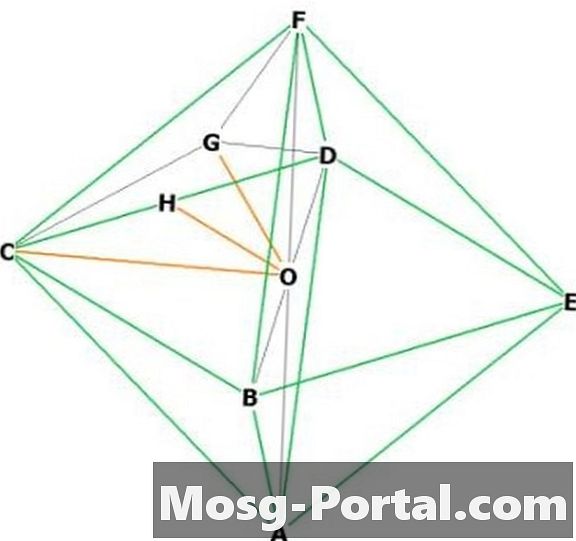
Изберете две съседни върхове, кажете „F“ и „C.“ "O" е в центъра. FOC е равнобедрен десен триъгълник с основа "a", така че OC и OF имат дължина a / sqrt (2) от теоремата на Питагор. Значи височина = a / sqrt (2).
Значи обемът на обикновен октаедър е 2 * (a ^ 2) * a / sqrt (2) / 3 = a ^ 3 * sqrt (2) / 3.
Площ
Редовната повърхност на октаедрите е площта на равностранен триъгълник от страна "а", пъти 8 лица.
За да използвате Питагоровата теорема, пуснете линия от върха към основата. Това създава два десни триъгълника с хипотенуза с дължина "a" и дължина на едната страна "a / 2". Следователно третата страна трябва да бъде sqrt = sqrt (3) a / 2. Значи площта на равностранен триъгълник е височина * основа / 2 = sqrt (3) a / 2 * a / 2 = sqrt (3) a ^ 2/4.
С 8 страни повърхността на обикновен октаедър е 2 * sqrt (3) * a ^ 2.